1.-GAUSS
2.- GAUSS JORDAN
Algoritmo de eliminación de Gauss-Jordan
- Ir a la columna no cero extrema izquierda
- Si el primer renglón tiene un cero en esta columna, intercambiarlo con otro que no lo tenga
- Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él
- Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en la forma de escalón)
- Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener un 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes
Ejemplo
Supongamos que es necesario encontrar los números x, y, z, que satisfacen simultáneamente estas ecuaciones:- Multiplicar una ecuación por un escalar no nulo.
- Intercambiar de posición dos ecuaciones
- Sumar a una ecuación un múltiplo de otra.
En nuestro ejemplo, eliminamos x de la segunda ecuación sumando 3/2 veces la primera ecuación a la segunda y después sumamos la primera ecuación a la tercera. El resultado es:
Primero:
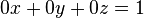 , es decir,
, es decir,  que no tiene solución.
que no tiene solución./////////////////////////CODIGO DE LEIMINACION DE GAUSS
#include <iostream.h>
#include <conio.h>
#include <stdlib.h>
#include <stdio.h>
#define N 10
float m[N][N+1], m1[N][N+1], X[N];
void obtenerm(int n), imprimirm(int matriz,int n);
void mfila(float factor,int fila, int n);
void sumarfilas(float factor,int fila1, int fila2, int n);
float sumarX(int n,int fila);
void obtenerinc(int n);
void gauss(int n);
void main(void)
{
int n;
cout<<"\tM E T O D O D O D E G A U S S"<<endl<<endl;
cout<<"Introduce el Tamanio de la Matriz (cuadrada nxn)\n n= ";
cin>>n;
obtenerm(n);
cout<<"\nLa matriz aumentada es:"<<endl;
imprimirm(0,n);
cout<<"\nSe usara el metodo de Gauss para obtener las incognitas"<<endl;
gauss(n);
getch();
}
void obtenerm(int n)
{
int i,j;
cout<<"Introduce los coeficientes de la matriz (aumentada):"<<endl;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
printf("\na[%d,%d]= ",i+1,j+1);
cin>>m[i][j];
}
printf("\nb%d= ",i+1);
cin>>m[i][j];
}
}
void imprimirm(int matriz, int n)
{
int i,j;
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
if(matriz==0)
printf("%5.2f ",m[i][j]);
else
printf("%5.2f ",m1[i][j]);
}
if(matriz==0)
printf("| %5.2f \n",m[i][j]);
else
printf("| %5.2f \n",m1[i][j]);
}
getch();
}
void mfila(float factor,int fila, int n)
{
int i;
for(i=0;i<=n;i++)
m1[fila][i]=m1[fila][i]*factor;
printf("\nSe multiplico la fila %d por el factor %4.1f, para obtener un 1 en la diagonal principal\n",fila+1,factor);
imprimirm(1,n);
}
void sumarfilas(float factor,int fila1, int fila2, int n)
{
int i;
for(i=0;i<=n;i++)
m1[fila2][i]=m1[fila1][i]*factor+m1[fila2][i];
printf("\nSe multiplico la fila %d por el factor %5.2f",fila1+1,factor);
printf("\nSe sumo la fila multiplicada (%d) a la fila %d\n",fila1+1,fila2+1);
imprimirm(1,n);
}
float sumarX(int n,int fila)
{
float suma=0;
int i;
for(i=0;i<n;i++)
suma=suma+(X[i]*m1[fila][i]);
return suma;
}
void obtenerinc(int n)
{
int i;
for(i=0;i<n;i++)
X[i]=0;
X[n-1]=m1[n-1][n];
for(i=n-2;i>=0;i--)
{
X[i]=m1[i][n]-sumarX(n,i);
}
}
void copiar(int n)
{
int i,j;
for(i=0;i<n;i++)
for(j=0;j<=n;j++)
m1[i][j]=m[i][j];
}
void gauss(int n)
{
int i,j,k;
float a;
copiar(n);
for(i=0;i<n;i++)
{
if(m1[i][i]==0)
{
//asdfjlkasdjklf
exit(0);
}
a=1/m1[i][i];
mfila(a,i,n);
j=i;
for(k=i+1;k<n;k++)
{
a=-m1[k][j];
sumarfilas(a,i,k,n);
}
}
printf("\nLa matriz despues de aplicar el metodo es:\n");
imprimirm(1,n);
obtenerinc(n);
printf("\nLos valores de las incognitas son:");
for(i=0;i<n;i++)
printf("\nx%d = %5.2f",i+1,X[i]);
}



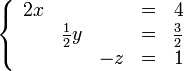





No hay comentarios:
Publicar un comentario