RESOLUCIÓN DE SISTEMAS
DE ECUACIONES LINEALES
INTRODUCCIÓN
En las distintas ramas de la ingeniería se plantean problemas en que se hace necesario resolver sistemas de ecuaciones lineales simultáneas con un número bastante grande de ecuaciones como para resolverlo manualmente o con calculadora, por lo que hemos de conocer algunos métodos directos e iterativos fáciles de programar para resolverlos con ayuda de la computadora.OBJETIVOS
1. Comprender y aplicar fluidamente, los métodos para resolver un sistema de ecuaciones lineales simultáneas por cumputadora.
· Métodos Directos2. Diferenciar las ventajas y desventajas de cada uno de los métodos.
»Eliminación de Gauss-Jordan· Métodos Iterativos
»Inversión de matrices
»Gauss-Seidel
DEFINICIONES
ECUACIÓN ALGEBRÁICA LINEAL
Es aquella en donde en cada término de la ecuación aparece únicamente una variable o incógnita elevada a la primera potencia. Por ejemplo:| a 11 X1 + a 12 X2 + a 13 X3 + ... + a 1n Xn = C1 | (1) |
SISTEMA DE ECUACIONES
Es un conjunto de ecuaciones que deben resolverse simultáneamente. En los sucesivo se considerarán únicamente sistemas de ecuaciones algebráicas lineales, o sea conjuntos de ecuaciones de la forma:| a11 X 1 + a 12 X2 + a13 X 3 +... + a 1n X n = C 1 | (a) | |||
| a 21 X 1 + a 22 X 2 + a 23 X 3 +... + a 2n X n = C 2 | (b) | (2) | ||
| ... | ||||
| a n1 X 1 + a n2 X 2 + a n3 X 3 + ... + a nn X n = C n | (c) |
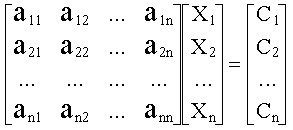 |
(3) |
| A X = C | (4) |
Entonces la matriz ampliada será:
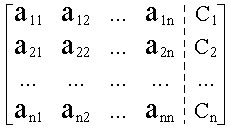 |
(5) |
SOLUCIÓN DE UN SISTEMA DE ECUACIONES
Es un conjunto de valores de las incógnitas que verifican simultáneamente a todas y cada una de las ecuaciones del sistema.De acuerdo con su solución, un sistema puede ser: Consistente, si admite solución; o Inconsistente, si no admite solución.
Un sistema Consistente puede ser: Determinado, si la solución es única o Indeterminado, si la solución no es única. En este caso se demuestra que existe una infinidad de soluciones.
TEOREMAS SOBRE RANGOS
El rango de una matriz es el orden de determinante no nulo de mayor orden que puede obtenerse de esa matriz. El rango de la matriz A se representa con la notación r(A) y el de la matriz ampliada con r(A, C).En álgebra se demuestra que:
- Para cualquier sistema,
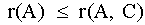
- Si r(A) < r(A, C) el sistema es inconsistente
- Si r(A) = r(A, C) el sistema de ecuaciones es consistente
En general, hay dos tipos de técnicas numéricas para resolver ecuaciones simultáneas: Directas, que son finitas; e Indirectas, que son infinitas.
Naturalmente, ninguna técnica práctica puede ser infinita. Lo que queremos decir es que en un principio los métodos directos (despreciando errores por redondeo) producirán una solución exacta, si la hay, en un número finito de operaciones aritméticas.
Por otra parte, un método indirecto requerirá en principio un número infinito de operaciones aritméticas para producir una solución exacta. Dicho de otra manera, un método indirecto tiene un error por truncamiento mientras que un método directo no lo tiene.
Sin embargo, la expresión "en principio" del párrafo anterior es crucial: en realidad se tienen errores por redondeo. Tendremos que considerar más cuidadosamente esta cuestión. En un sistema grande, mal comportado, los errores por redondeo de un método directo puede hacer que la "solución" carezca de sentido. A pesar de su error teórico por truncamiento, un método indirecto puede ser mucho más deseable porque en él los errores por redondeo no se acumulan.
MÉTODO DE ELIMINACIÓN DE GAUSS
El primer método que se presenta usualmente en álgebra, para la solución de ecuaciones algebricas lineales simultáneas, es aquel en el que se eliminan las incógnitas mediante la combinación de las ecuaciones. Este método se conoce como Método de Eliminación. Se denomina eliminación Gaussiana si en el proceso de eliminación se utiliza el esquema particular atribuido a Gauss.Utilizando el método de Gauss, un conjunto de n ecuaciones con n incógnitas se reduce a un sistema triangular equivalente (un sistema equivalente es un sistema que tiene iguales valores de la solución), que a su vez se resuelve fácilmente por "sustitución inversa"; un procedimiento simple que se ilustrará con la presentación siguiente.
El esquema de Gauss empieza reduciendo un conjunto de ecuaciones simultáneas, tal como se muestra en (2), a un sistema triangular equivalente como:
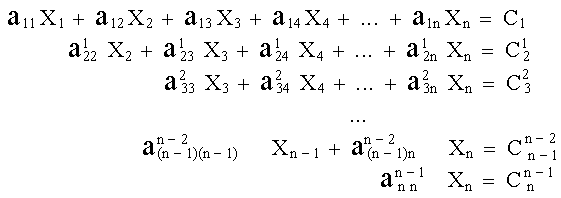
|
(6) |
1. La primera ecuación (2) se divide entre el coeficiente de X1 en esa ecuación para obtener:
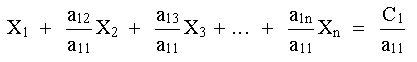
|
(7) |
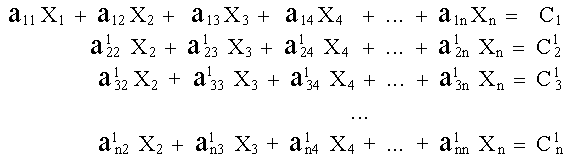 |
(8) |
2. Siguiendo los pasos anteriores, la segunda ecuación (8) se convierte en la ecuación pivote, y los pasos de la parte 1 se repiten para eliminar X2 de todas las ecuaciones que siguen a esta ecuación pivote.
Esta reducción nos conduce a:
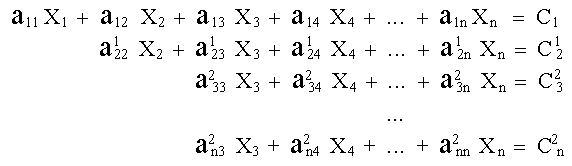
|
(9) |
4. Una vez obtenido el conjunto triangular de ecuaciones, la última ecuación de este conjunto equivalente suministra directamente el valor de Xn (ver ec. 6). Este valor se sustituye entonces en la antepenúltima ecuación del conjunto triangular para obtener un valor de Xn-1, que a su vez se utiliza junto con el valor de Xn en la penúltima ecuación del conjunto triangular para obtener un valor Xn-2 y asi sucesivamente. Este es el procedimiento de sustitución inversa al que nos referimos previamente.
Para ilustrar el método con un conjunto numérico, apliquemos estos procedimientos a la solución del siguiente sistema de ecuaciones:
| X1 + 4 X2 + X3 = 7 | ||
| X1 + 6 X2 - X3 = 13 | (10) | |
| 2 X1 - X2 + 2 X3 = 5 |
| X1 + 4 X2 + X3 = 7 | ||
| 2 X2 - 2 X3 = 6 | (11) | |
| 9 X2 + (0) X3 = -9 |
| X1 + 4 X2 + X3 = 7 | ||
| 2 X2 - 2 X3 = 6 | (12) | |
| - 9 X3 = 18 |
DESVENTAJAS DEL MÉTODO DE ELIMINACIÓN
1. DIVISIÓN ENTRE CEROUna de sus desventajas es que durante el proceso en las fases de eliminación y sustitución es posible que ocurra una división entre cero. Se ha desarrollado una estrategia del pivoteo para evitar parcialmente estos problemas. Ésta se deja como investigación al alumno.
2. ERRORES DE REDONDEO
La computadora maneja las fracciones en forma decimal con cierto número limitado de cifras decimales, y al manejar fracciones que se transforman a decimales que nunca terminan, se introduce un error en la solución de la computadora. Este se llama error por redondeo.
Cuando se va a resolver solamente un pequeño número de ecuaciones, el error por redondeo es pequeño y generalmente no se afecta sustancialmente la presición de los resultados, pero si se van a resolver simultáneamente muchas ecuaciones, el efecto acumulativo del error por redondeo puede introducir errores relativamente grandes en la solución. Por esta razón el número de ecuaciones simultáneas que se puede resolver satisfactoriamente con el método de eliminación de Gauss, utilizando de 8 a 10 dígitos significativos en las operaciones aritméticas, se limita generalmente a 15 o 20.
3. SISTEMAS MAL CONDICIONADOS
La obtención de la solución depende de la condición del sistema. En sentido matemático, los sistemas bien condicionados son aquellos en los que un cambio en uno o más coeficientes provoca un cambio similar en la solución. Los sistemas mal condicionados son aquellos en los que cambios pequeños en los coeficientes provocan cambios grandes en la solución.
Una interpretación diferente del mal condicionamiento es que un rango amplio de respuestas puede satisfacer aproximadamente al sistema. Ya que los errores de redondeo pueden inducir cambios pequeños en los coeficientes, estos cambios artificiales pueden generar errores grandes en la solución de sistemas mal condiconados.
MÉTODO DE GAUSS - JORDAN
Este método, que constituye una variación del método de eliminación de Gauss, permite resolver hasta 15 o 20 ecuaciones simultáneas, con 8 o 10 dígitos significativos en las operaciones aritméticas de la computadora. Este procedimiento se distingue del método Gaussiano en que cuando se elimina una incógnita, se elimina de todas las ecuaciones restantes, es decir, las que preceden a la ecuación pivote así como de las que la siguen.El método se ilustra mejor con un ejemplo. Resolvamos el siguiente conjunto de ecuaciones
3.0 X1 - 0.1 X2 - 0.2 X3 = 7.8500
0.1 X1 + 7.0 X2 - 0.3
X3 = - 19.3
0.3 X1 - 0.2 X2 + 10 X3 = 71.4000
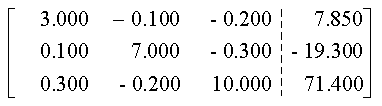
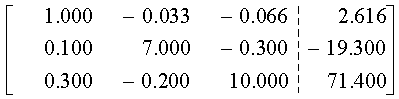
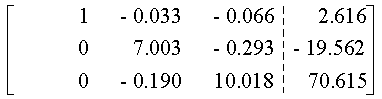
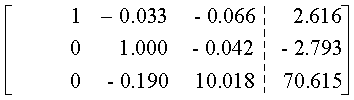
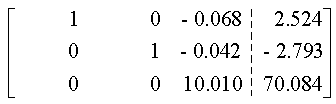
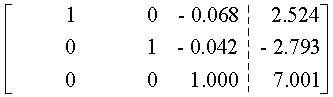
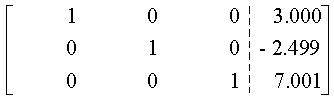
Las ventajas y desventajas de la eliminación gaussiana se aplican también al método de Gauss-Jordan.
Aunque los métodos de Gauss-Jordan y de eliminación de Gauss pueden parecer casi idénticos, el primero requiere aproximadamente 50% menos operaciones. Por lo tanto, la eliminación gaussiana es el mé todo simple por excelencia en la obtención de soluciones exactas a las ecuaciones lineales simultáneas. Una de las principales razones para incluir el método de Gauss-Jordan, es la de proporcionar un método directo para obtener la matriz inversa.
INVERSIÓN DE MATRICES
Sea A una matriz cuadrada no singular, es decir, que su determinante sea diferente de cero, |A|≠0. Por definición de matriz inversa, se tiene que A-1 es la inversa de A si:|
|
(13) |
| A X = I | (14) |
Por lo anterior, es posible determinar la inversa de una matriz con el método de Gauss-Jordan de eliminación completa. Para lograrlo, bastará con aplicar las operaciones elementales sobre los renglones de la matriz ampliada (A, I) de manera de transformar A en I. Cuando se haya hecho, se obtendrá la matriz ampliada (I, A-1) , con lo que se tendrá la inversa buscada.
EJEMPLO
Invertir la matriz
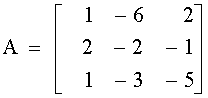
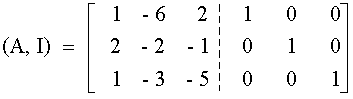
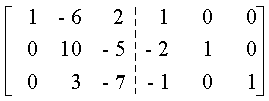
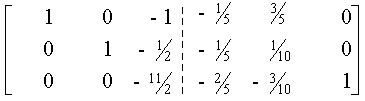
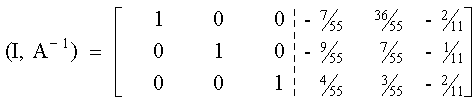
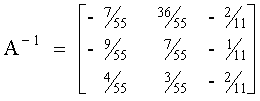
Comparando ambos métodos, es evidente que el método de inversión de matrices no es práctico para la solución de un sólo conjunto (o dos o tres conjuntos) de ecuaciones simultáneas, porque la cantidad de cálculos que intervienen para determinar la matriz inversa es muy grande. Sin embargo, si se desea resolver 20 conjuntos de 10 ecuaciones simultáneas que difieren únicamente en sus términos independientes, una matriz aumentada que contiene 20 columnas de constantes (que se utilizarían en el método de eliminación) sería difícil de reducir, y se podría usar con ventaja el método de inversión de matrices.
No hay comentarios:
Publicar un comentario